Microsoft Excel ist ein Dienstprogramm, das in vielen Unternehmen und Unternehmen weit verbreitet ist. Die Realität sieht so aus, dass fast jeder Mitarbeiter in gewissem Maße Excel-Kenntnisse haben muss, da mit diesem Programm die unterschiedlichsten Aufgaben gelöst werden. Bei der Arbeit mit Tabellen ist es oft notwendig festzustellen, ob bestimmte Variablen zusammenhängen. Dazu wird die sogenannte Korrelation verwendet. In diesem Artikel werden wir uns genauer ansehen, wie der Korrelationskoeffizient in Excel berechnet wird. Lass es uns herausfinden. Gehen!
Beginnen wir mit dem Korrelationskoeffizienten im Allgemeinen. Es zeigt den Grad der Beziehung zwischen zwei Elementen an und reicht immer von -1 (starke inverse Beziehung) bis 1 (starke direkte Beziehung). Wenn der Koeffizient 0 ist, bedeutet dies, dass keine Beziehung zwischen den Werten besteht..
Nachdem wir uns mit der Theorie beschäftigt haben, gehen wir nun zur Praxis über.
Ermittlung des Koeffizienten durch den "Funktionsassistenten"
Um die Beziehung zwischen den Variablen x und y zu finden, verwenden Sie die eingebaute Funktion von Microsoft Excel "CORREL". Gehen Sie dazu folgendermaßen vor:
- Wählen Sie die Zelle aus, in der das Berechnungsergebnis angezeigt werden soll, und klicken Sie auf die Schaltfläche des Funktionsassistenten (befindet sich neben dem Feld für Formeln).
- Wählen Sie im sich öffnenden Fenster aus der Liste der Funktionen "CORREL" aus und klicken Sie auf "OK".
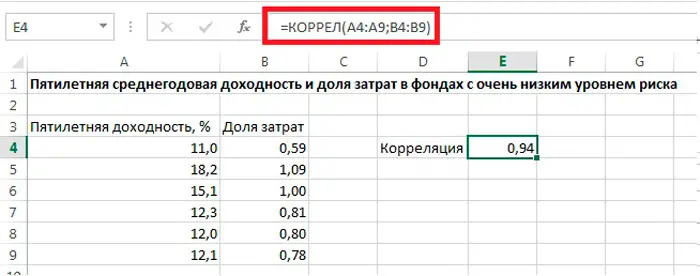
- Legen Sie danach im Funktionsargumentenfenster den Bereich in den Feldern "Array1" und "Array2" fest. Markieren Sie beispielsweise für Array1 die y-Werte und für Array2 die x-Werte.
In unserem Beispiel tragen wir in der Zeile "Array1" die Koordinaten des Zellenbereichs des Wertes ein, dessen Abhängigkeit ermittelt werden soll (in unserem Fall sind dies Umsatzerlöse). Um die Adresse des Arrays zum Feld hinzuzufügen, wählen Sie die Zellen in der Spalte aus. In der Zeile „Array2“ sollten Sie die Koordinaten einer weiteren Spalte eintragen (in unserem Fall das vorgesehene Werbebudget). Unten im Punkt "Wert" sehen Sie sofort das Ergebnis der Berechnung. Klicken Sie nach dem Hinzufügen von Daten zu den Feldern "Array1" und "Array2" auf "OK"..
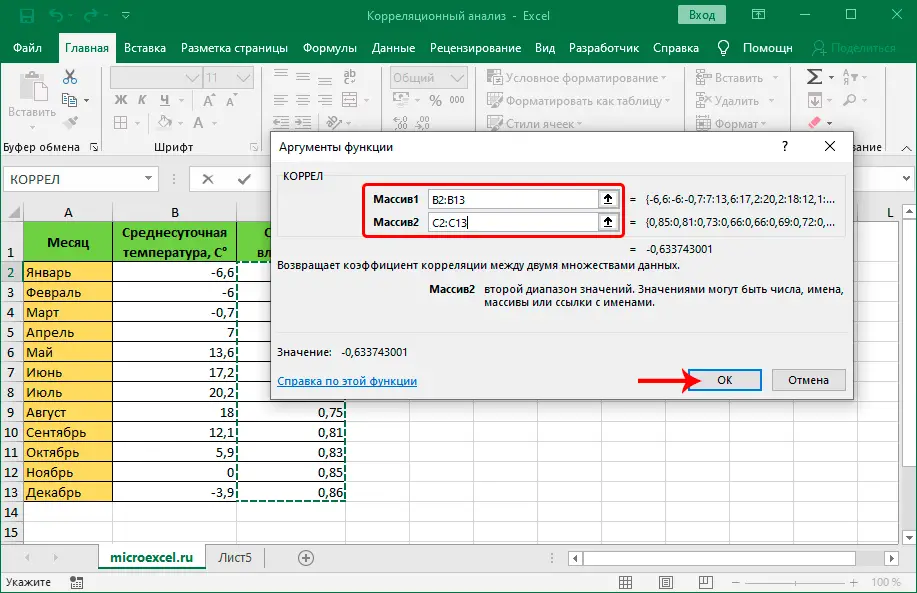
- Als Ergebnis erhalten Sie den vom Programm berechneten Korrelationskoeffizienten in der zuvor ausgewählten Zelle.
In unserem Fall ist der Indikator durchschnittlich, die Abhängigkeit der Rentabilität von der Werbung ist nicht beeindruckend, obwohl sie definitiv vorhanden ist.
Korrelationsberechnung mit den Werkzeugen des Analysepakets
Die Korrelationsabhängigkeit kann auch mit einem speziellen Tool berechnet werden, nachdem es zuvor aktiviert wurde. Um die Aufgabe abzuschließen, müssen Sie die folgenden Manipulationen durchführen:
- Gehen Sie vom Menü Datei zum Abschnitt Optionen.
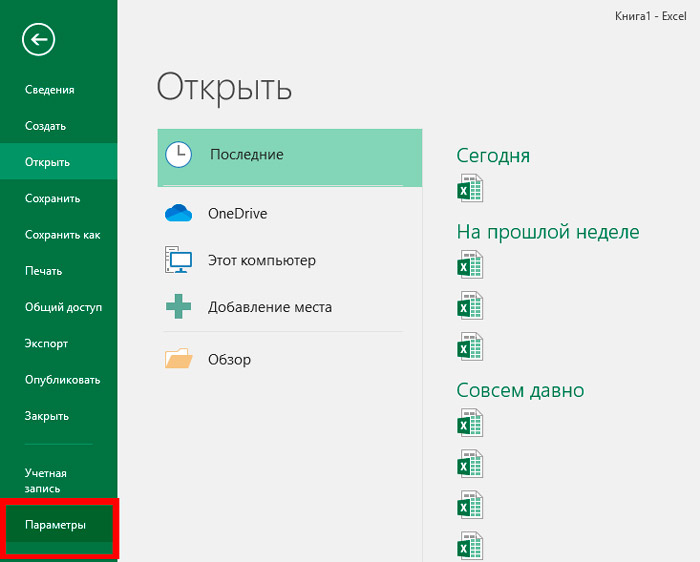
- Gehen Sie im Menü auf der linken Seite zum Abschnitt "Add-ons".
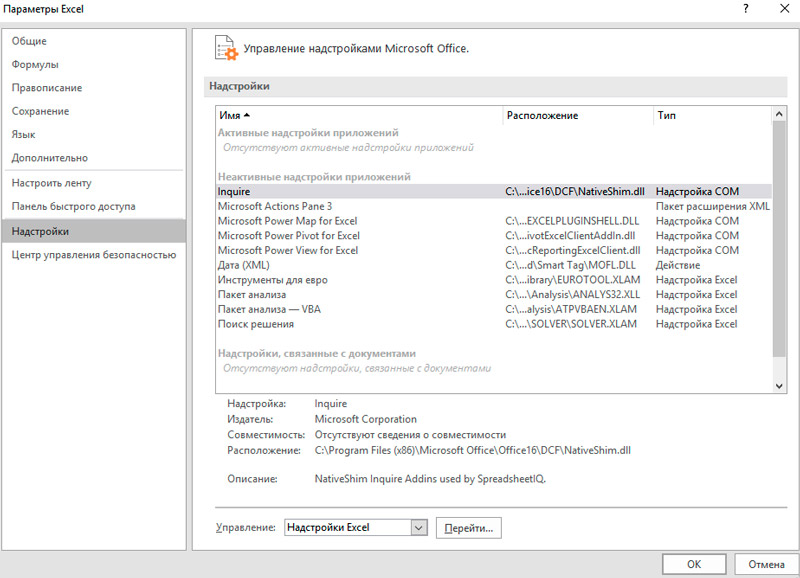
- Unten im Fenster müssen Sie im Block "Verwaltung" "Excel-Add-Ins" einstellen (falls anders eingestellt, ändern) und zu den Add-Ins gehen.
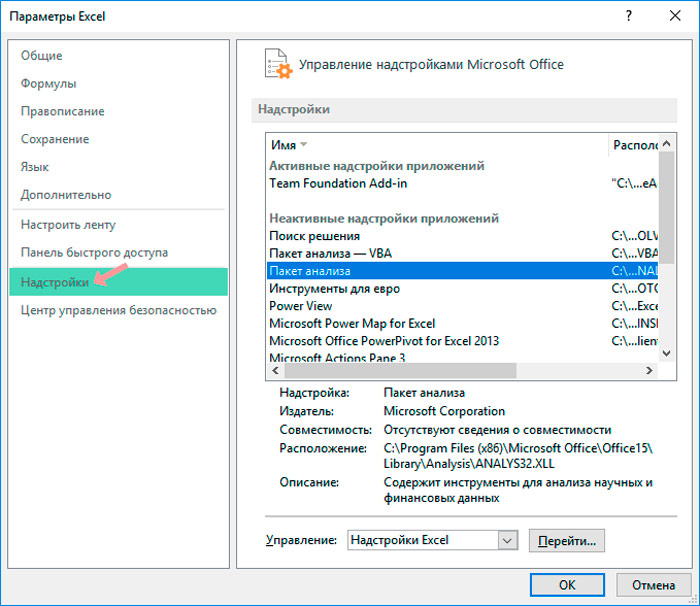
- Markieren Sie im sich öffnenden Add-On-Fenster das "Analysepaket" und klicken Sie auf "OK", um das Toolkit zu aktivieren.
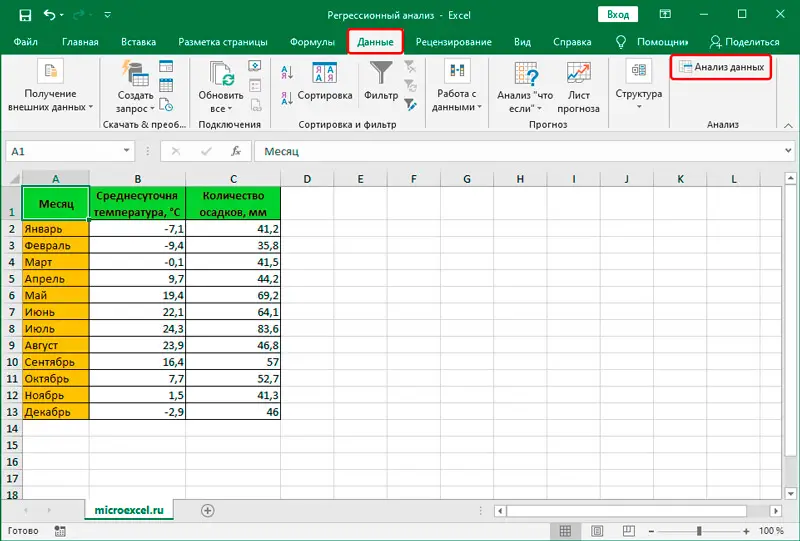
- Gehen Sie nun auf die Registerkarte "Daten" - ein weiterer Block von "Analyse"-Tools wird auf der Multifunktionsleiste verfügbar sein. Klicken Sie hier auf "Datenanalyse".
- Wählen Sie unter den vorgeschlagenen Optionen "Korrelation" und klicken Sie auf "OK", woraufhin die erforderlichen Einstellungen verfügbar sind.
- In dem sich öffnenden Fenster sollten Sie in der Zeile "Eingabeintervall" das Intervall aller an der Berechnung der Abhängigkeit beteiligten Spalten gleichzeitig eingeben.
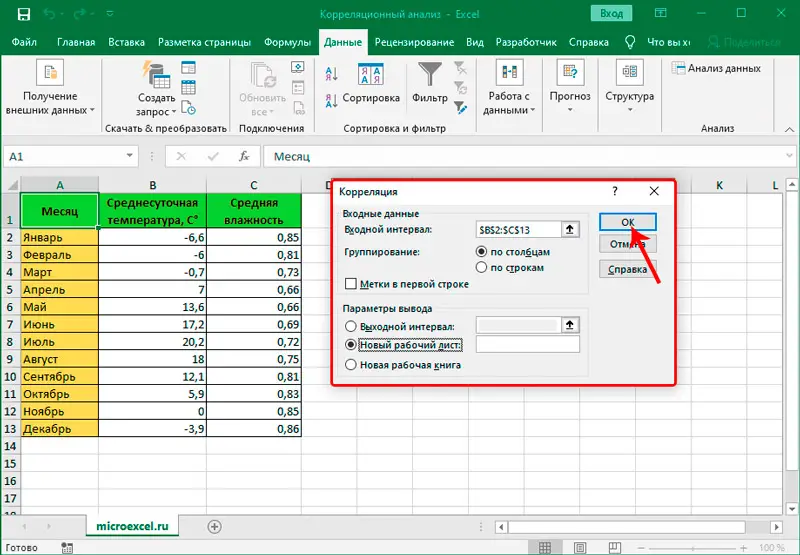
- Belassen Sie Gruppierung als Spalten, da die Daten in unserem Beispiel in Spalten und nicht Zeile für Zeile unterteilt sind.
- In den Parametern der Ergebnisausgabe können Sie die Standardeinstellung "Neues Arbeitsblatt" belassen (die Daten werden auf einem neuen Blatt angezeigt) oder "Ausgabeintervall" auswählen und die Koordinaten der Zellen in der Zeile angeben, damit der Koeffizient erscheint an der angegebenen Stelle auf der Seite. Sie können auch die Summe der Berechnungen in einer neuen Arbeitsmappe anzeigen, indem Sie die Markierung auf das entsprechende Element bewegen.
- Nachdem Sie die erforderlichen Einstellungen vorgenommen haben, klicken Sie auf "OK" und erhalten Sie die Ergebnisse der durchgeführten Arbeiten. Es unterscheidet sich nicht von dem, was mit der ersten Berechnungsmethode erhalten wurde, denn obwohl die Schritte unterschiedlich sind, führt das Programm die gleichen Berechnungen durch.
Der Korrelationskoeffizient wird vom Programm berechnet
Berechnung der Korrelationsabhängigkeit nach der Formel
Die nächste Methode wird für Studenten relevant sein, die eine Abhängigkeit nach einer bestimmten Formel finden müssen. Zunächst müssen Sie die Durchschnittswerte der Variablen x und y kennen, wonach Sie anhand der erhaltenen Daten die Beziehung berechnen können:
- Markieren Sie die Variablenwerte und verwenden Sie die Funktion MITTELWERT.
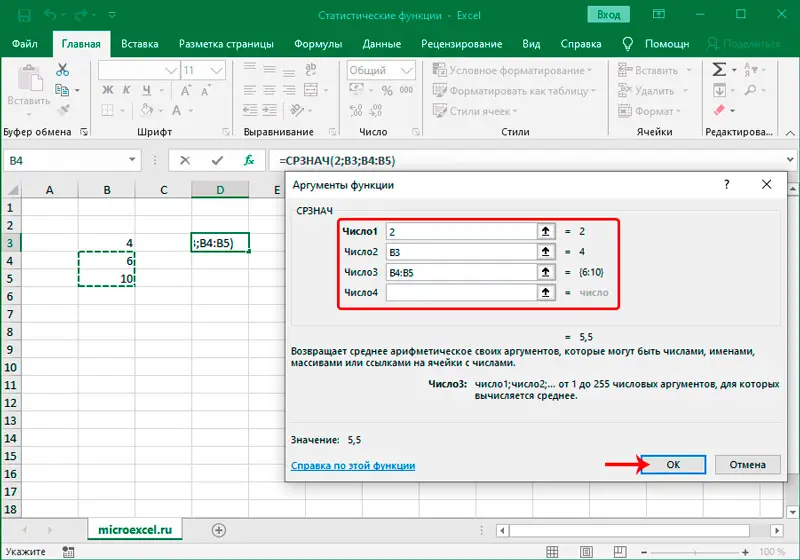
- Als nächstes müssen Sie die Differenz zwischen jedem x und x av und y av berechnen . Schreiben Sie in die ausgewählten Zellen die Formeln xx, y-. Vergessen Sie nicht, die Zellen mit Durchschnittswerten einzufrieren. Dann strecken Sie die Formel nach unten, so dass sie auf den Rest der Zahlen zutrifft.
- Da Sie nun alle benötigten Daten haben, können Sie die Korrelation berechnen. Multiplizieren Sie die resultierenden Differenzen wie folgt: (xx avg ) * (yy avg ). Nachdem Sie das Ergebnis für jede der Variablen erhalten haben, fügen Sie die resultierenden Zahlen mit der Autosum-Funktion hinzu. So wird der Zähler berechnet.
- Kommen wir nun zum Nenner. Die berechneten Differenzen müssen quadriert werden. Tragen Sie dazu die Formeln in eine separate Spalte ein: (xx av ) 2 und (yy av ) 2 . Dann dehnen Sie die Formeln auf den vollen Bereich aus. Ermitteln Sie dann mit der Schaltfläche "AutoSum" die Summe für alle Spalten (für x und für y).
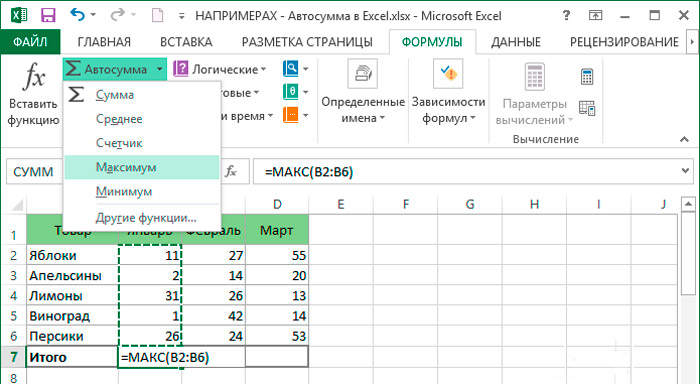
- Es bleibt, die gefundenen Summen zu multiplizieren und daraus die Quadratwurzel zu ziehen.
- Der letzte Schritt besteht darin, den Zähler durch den Nenner zu dividieren. Das erhaltene Ergebnis ist der gewünschte Korrelationskoeffizient.
Wie Sie sehen, können Sie die Berechnung komplexer mathematischer Ausdrücke erheblich vereinfachen, wenn Sie wissen, wie Sie mit den Funktionen von Microsoft Excel richtig arbeiten. Dank der im Programm implementierten Tools können Sie Korrelationsanalysen in Excel in nur wenigen Minuten durchführen und sparen Zeit und Mühe. Schreiben Sie in die Kommentare, wenn der Artikel Ihnen geholfen hat, das Problem zu verstehen, fragen Sie nach allem, was Sie zu dem betrachteten Thema interessiert hat..